이번 포스팅에서는 진리표를 불대수식으로 바꾸는 방법 두 가지를 알아보자.
1. 표준 논리곱의 합
바꾸는 방법
ㄱ. 1이 되는 경우
ㄴ. 각 행에 대해 그 행에서만 1이 되는 곱
ㄷ. ㄴ의 곱들을 다 더하기
이렇게만 보면 와닿지 않을 수 있다. 직접 해보자.

위와 같은 진리표에서, 1이 되는 경우는
011, 100, 101, 110, 111이고, 각 항에 대해 그 행에서만 1이 되는 곱은
011 = A'BC
100 = AB'C'
101 = AB'C
110 = ABC'
111 = ABC
이 곱들을 모두 더하면,
A'BC + AB'C' + AB'C + ABC' + ABC
가 된다.
이 식은, 위의 다섯가지 경우에서는 1이 되고, 나머지 세가지 경우에서는 0이 되므로,
F가 표현하고자 하는 동작과 정확히 일치한다.
따라서 F = A'BC + AB'C' + AB'C + ABC' + ABC 로 나타낼 수 있다.
최소항이란
각 변수가 그대로 혹은 보수 형태로 한번씩 나타나는 곱
예를 들어,
A,B,C 세개의 변수가 있을 때,
A'BC' : 최소항이다.
A'B : 최소항이 아니다. C가 없기 때문이다.
A'BC'B : 최소항이 아니다. B가 두 번 있기 때문이다. (물론 간략화가 가능하지만, 현재 상태에서는 아니다.)
표기 방법

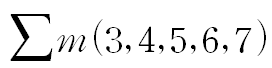
2. 표준 논리합의 곱
바꾸는 방법
ㄱ. 0이 되는 경우
ㄴ. 각 행에 대해, 그 행에서만 0이 되는 합
ㄷ. ㄴ의 합들을 다 곱하기
앞서 표준 논리곱의 합과의 차이점이 보일 것이다.
이번에도 예를 들어 알아보자.

위의 표에서, 0이 되는 경우는
000, 001, 010이고, 각 항에 대해 그 행에서만 0이 되는 합은
000 -> A+B+C
001 -> A+B+C'
010 -> A+B'+C
(1이 되는 애들을 뒤집으면 됨.)
이 합들을 모두 곱하면
(A+B+C)(A+B+C')(A+B'+C)
가 된다.
이 식은, 위의 세가지 경우에서는 0, 나머지 경우에서는 1이므로 F의 동작을 정확히 반영한다.
따라서 F = (A+B+C)(A+B+C')(A+B'+C) 와 같이 표현할 수 있다.
최대항이란
각 변수가 그대로 혹은 보수 형태로 한번씩 나타나는 합
예를 들어,
A,B,C 세개의 변수가 있을 때,
A+B'+C : 최대항이다.
A+B : 최대항이 아니다. C가 없기 때문이다.
A+B'+C+C : 최대항이 아니다. C가 두 번 있기 때문이다. (물론 간략화가 가능하지만, 현재 상태에서는 아니다.)
표기 방법


* 최소항의 부정은 최대항, 최대항의 부정은 최소항이다.
