💡 구간 합 알고리즘이란?
일반적으로 일정 범위의 합을 구하는 시간 복잡도는 O(N)입니다.
한 번 합을 구하는 거야 그냥 하던대로 합을 구하면 되겠지만, 아주 여러번 그 합을 구해야 한다면 시간복잡도가 펑펑펑 늘어나겠죠?? 이런 경우에 시간 복잡도를 줄이기 위해 합 배열을 구현해놓고 인덱스로 접근하여 O(1)의 시간복잡도로 빠르게 합을 구하는 것이 바로 구간 합 알고리즘입니다.
💡 합 배열 정의하기
합 배열을 그림으로 살펴봅시다.

그림에서 알 수 있듯, 합 배열은 i번째까지의 합을 저장해둔 배열입니다.
S[i] = A[0] + A[1] + A[2] + ... + A[i-1] + A[i]
입니다.
예를 들어, S[2]는 A[0] + A[1] + A[2] = 15 + 13 + 10 = 38이 되겠죠.
이것은 곧 다음의 식과 같습니다.
S[i] = S[i-1] + A[i]
💡 합 배열을 이용하여 구간 합 구하기
A[2]부터 A[5]까지의 합을 합배열을 사용해서 구하려면 어떻게 해야할까요?
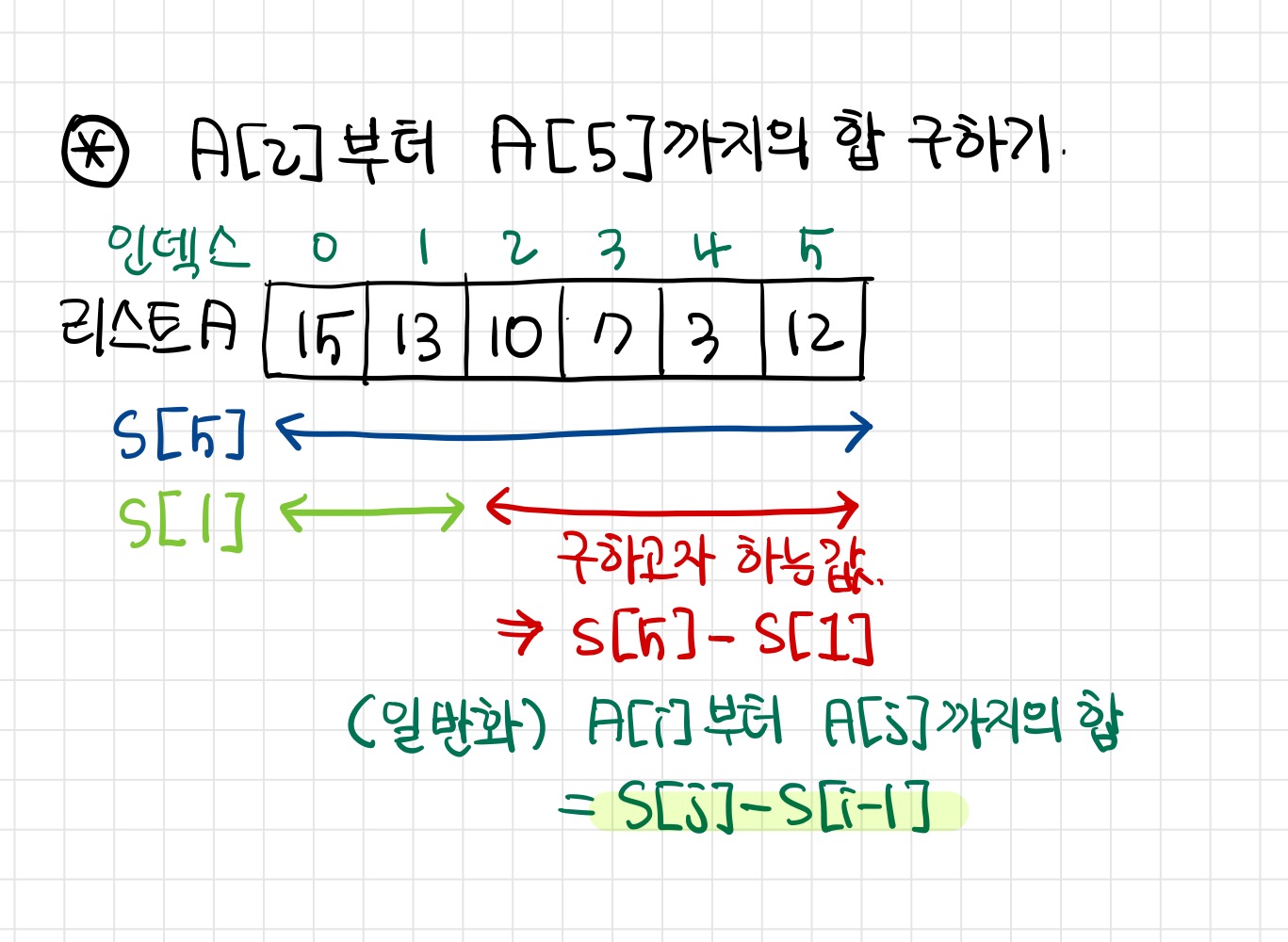
S[5]에서 S[1]을 빼주면 됩니다.
이것을 일반화 하면
A[i]부터 A[j]까지의 합 = S[j] - S[i-1]
임을 알 수 있습니다.
📌 예제) 백준 11659번. 구간 합 구하기 4


이 문제에서 수의 개수와 합을 구해야 하는 횟수는 최대 100,000개입니다.
평소에 하던 것처럼 구간마다 합을 매번 계산하게 된다면 절대 제한 시간 내에 계산을 끝낼 수 없습니다.
이럴 때 사용하는 것이 구간 합 알고리즘인데요.
일단 n, m을 입력받고,
n개의 숫자를 입력받아 리스트로 만드는 코드를 작성해줍니다.
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
nums = list(map(int, input().split()))sys.stdin.readline을 쓰는 이유는 입력을 드는 시간을 최소화 하기 위함입니다.
sys.stdin.readline에 대해 더 알고싶다면
2022.09.16 - [📂 Language/Python] - [Python] 파이썬 input 시간 초과뜰 때 sys.stdin.readline 사용하기
이 글을 참고해주세요!!
이제 구간 합 리스트를 선언해줍니다.
prefix_sum = [0]이때, 리스트에 미리 0을 넣어두는 이유는 문제에서 인덱스가 1로 시작하는데, 파이썬의 인덱스는 0부터 시작하므로 시작 인덱스를 1로 맞추어 좀 더 편하게 구현하기 위함입니다.
입력받음과 동시에 합 배열을 채워나가기 위해 temp 변수를 선언해줍니다.
temp 변수는 합을 저장하는 변수로서의 역할을 합니다.
temp = 0
다음으로 사용자에게 입력 받은 숫자 리스트를 이용해 합배열을 만듭니다.
for i in nums:
prefix_sum.append(temp + i)
temp += i여기까지 하면 합배열이 완성 되는데요.
이후 m번의 입력에서 구간합을 구할 시작 인덱스와 끝 인덱스를 받습니다.
구간합을 구하는 공식은 S[i] = S[i-1] + A[i]라는 것을 이용해 구간합을 출력해주는 코드를 작성합니다.
for _ in range(m):
i, j = map(int, input().split())
print(prefix_sum[j] - prefix_sum[i-1])
전체 코드
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
nums = list(map(int, input().split()))
prefix_sum = [0]
temp = 0
for i in nums:
prefix_sum.append(temp + i)
temp += i
for _ in range(m):
i, j = map(int, input().split())
print(prefix_sum[j] - prefix_sum[i-1])
💡 2차원 리스트 합 배열 구하기

위와 같은 이차원 리스트가 있다고 생각해봅시다.
(2, 2)에서 (3, 4)까지의 합을 구하면 3 + 4 + 5 + 4 + 5 + 6 = 27이고,
(4, 4)에서 (4, 4)까지의 합을 구하면 7입니다.
2차원 구간의 합 배열을 D[x][y], 원본 배열을 A[x][y]라고 했을 때,
2차원 리스트의 합 배열을 구하는 방법은 다음과 같습니다.
1. 1행, 1열 채우기

1행, 1열을 채우는 방법은 일차원 리스트의 구간 합을 구하는 것과 거의 비슷합니다.
2. 나머지 값 채우기

위의 식을 일반화 해주면 D[i][j]를 구하는 공식은 다음과 같습니다.
D[i][j] = D[i-1][j] + D[i][j-1] - D[i-1][j-1] + A[i][j]
3. 구간 합 구하기 예
(2, 2)에서 (3, 4)까지의 구간합을 구한다고 생각해봅시다.
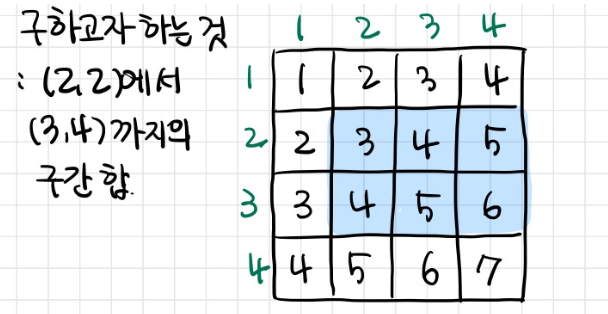
색칠된 구간의 합을 구하면 되겠죠??

D[3][4] - D[1][4] - D[4][1] + D[1][1]임을 알 수 있는데요,
이를 일반화 하면 (x1, y1)에서 (x2, y2)까지의 구간합을 구하는 공식은
D[X2][Y2] - D[X1-1][Y2] - D[X2][Y1-1] + D[X1-1][Y1-1]이 됩니다.
📌 예제) 백준 11660번. 구간 합 구하기 5

문제의 예시는 위의 예시와 같습니다.


이번에도 n, m을 입력 받는 건 동일합니다.
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
원본 배열 a와 합배열 d를 선언해줍니다.
a = [[0] * (n+1)]
d = [[0] * (n+1) for i in range(n+1)]n+1개를 만들어주는 이유는 1차원리스트 합배열을 선언할 때의 이유와 같습니다.
사용자에게 입력 받은 수들을 원본 배열에 넣어주는 코드를 작성합니다.
for i in range(n):
a_low = [0] + list(map(int, input().split()))
a.append(a_low)다음으로, 앞서 도출했던 합 배열을 구하는 공식을 적용해 합배열을 구해줍니다.
for i in range(1, n+1):
for j in range(1, n+1):
# 합 배열 구하기
d[i][j] = d[i][j-1] + d[i-1][j] - d[i-1][j-1] + a[i][j]마지막으로 구간합 공식을 적용해 사용자에게 입력 받은 좌표들로 구간합을 구하는 코드를 작성해줍니다.
for _ in range(m):
x1, y1, x2, y2 = map(int, input().split())
# 구간합 공식
res = d[x2][y2] - d[x1-1][y2] - d[x2][y1-1] + d[x1-1][y1-1]
print(res)전체 코드
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
# 합 배열 먼저 만들기
a = [[0] * (n+1)]
d = [[0] * (n+1) for i in range(n+1)]
for i in range(n):
a_low = [0] + list(map(int, input().split()))
a.append(a_low)
for i in range(1, n+1):
for j in range(1, n+1):
# 합 배열 구하기
d[i][j] = d[i][j-1] + d[i-1][j] - d[i-1][j-1] + a[i][j]
for _ in range(m):
x1, y1, x2, y2 = map(int, input().split())
# 구간합 공식
res = d[x2][y2] - d[x1-1][y2] - d[x2][y1-1] + d[x1-1][y1-1]
print(res)
